Eugene Molinelli, J.D., Ph.D.,
© 2019 Eugene Molinelli
Abstract.
The draft 2019 Revised Patent Subject Matter Eligibility Guidance (“draft Guidance”) should be modified to treat equations that relate physical phenomena involved in a man-made object, and steps that are not routinely performed mentally, as not per se abstract, but instead directed to a practical application that renders them patent eligible subject matter under 35 U.S.C. §101.
Discussion
Step 1 of the patent eligibility analysis is to determine if the claims are directed to one of the four categories listed in 35 U.S.C. §101 (process, machine, article of manufacture, composition of matter). If not, the claim is not eligible. If so, the process moves to the two-step Alice/Mayo process that has been implemented by the USPTO as steps 2A and 2B of the patent eligibility analysis. In step 2A it is determined whether the claim is directed to a judicial exception (laws of nature, natural phenomena, and abstract ideas) . If not, the claim is patent eligible and the application is examined under the other criteria (useful, new and non-obvious). If the claim is found during step 2A to be directed to a judicial exception, then in step 2B it is determined if there is something more than the judicial exception that provides the novelty.
,Software is often found to be directed to an abstract idea at step 2A. The claim is examined to determine whether there is “significantly more” at step 2B. In the draft Guidance recently published for public comment, the USPTO asserts “that abstract ideas can be grouped as, e.g., mathematical concepts, certain methods of organizing human activity, and mental processes.” The draft Guidance further asserts mathematical concepts include “mathematical relationships, mathematical formulas or equations, mathematical calculations” citing several cases that have addressed mathematical claims (draft Guidance, p. 9-10). The draft Guidance further asserts mental steps include “concepts performed in the human mind” (draft Guidance, p. 11).
This grouping is too broad because it sweeps into abstract ideas many useful software inventions that do not fit the factual patterns of the cited cases finding ineligible software claims. In fact, this grouping has the potential to be a per se prohibition on pure software inventions that is eschewed by the Alice decision; and explicitly rejected in the Federal Circuit (Enfish, LLC v. Microsoft Corp., 822 F.3d 1327 (Fed. Cir. 2016)) which states claims directed to software are not “inherently abstract” and too broad a grouping “otherwise risks . . . creating a categorical ban on software patents.” Enfish at 1335, 1339.
In many claims, a mathematical equation expresses the specificity that distinguishes the claimed process from generic computer processes such as “data analysis” and “correlation.” To automatically classify such an equation as abstract is to institute a catch 22 for the Applicant. The specificity and novelty are in the equation; and so, both are ignored in the examination of claims.
In the following, it is assumed that the equations operate on information input, e.g., information previously collected or stored; and, produce information output, e.g., the value(s) for some physical property that are not used to control a machine or transform a substance or article of manufacture or treat a patient. As proposed here, patent eligible software claims recite implementation on a computer/processor, with some output based on the result exported from the processor, either as data presented on a display or transmitted as a signal to a different component or device. In such claims, certain types of equation should be patent eligible under step 2A.
The new distinction that the USPTO, and judges, should consider under step 2A is whether the equation in the software is a mathematical identity or not. A mathematical identity is true, that is, the equality expressed by the equation holds, regardless of any physical phenomenon that might be represented by the variables x1, x2,… in the equation. It does not matter what physical phenomenon x represents, whether time, distance, mass, temperature, etc.. With this definition of a mathematical identity, there are two classes of equations that are used in software claims that influence whether the equation itself is an abstract idea.
- Mathematical identities.
1.1 (Not eligible) Mathematical identities simply evaluated on a computer.
This is the kind of equation found ineligible in Benson, which was implemented as an algorithm involving a series of steps, and simply converted a binary value (of zeros and ones) to a decimal value (of the digits 0 through 9) indicating the same numerical value. Such a conversion is true no matter what physical phenomenon the binary value or decimal value represents; it is a mathematical identity. There was no requirement, in claim 13 adjudicated by the SC in Benson, that the mathematical identity be confined to a particular computer operation, e.g., to retrieve digital data from a memory location and convert that value to decimal before storing on computer readable media, or presenting on a display, or sending to another component or device. Benson at 74.
1.2. (Eligible) Mathematical identities evaluated to cause computer operation.
It is inherent in the design of a general-purpose computer processor to perform operations that are agnostic as to the physical phenomenon being represented by the data. Such computer technologies rely on some mathematical identities. .Examples of such identities are the equations used in digital data compression, digital data transmission, digital data encryption, different digital implementation of a mathematical operation rather than used manually, e.g., Fast Fourier Transform for digital data, among others. However, unlike the claim in Benson, claims reciting these equations do not usurp all uses of the underlying mathematical identity. They are limited to how the computer operates during the process that has utility to the computer or computer system, e.g., the application of the process to compression, encryption, carrying out the evaluation, etc. This is the type of mathematical concept that should be patent eligible.
- Equalities among particular properties (not mathematical identities).
2.1. (Eligible) Equations for physical phenomena.
These equations are only true if the variables in the equations relate to particular physical phenomena. By definition, these are not mathematical identities. Example equations are employed for: inferring a value of a physical quantity from measurements of different physical quantities; changing a contour in a computer animation image based on a change in sounds, providing a segmentation boundary for a particular organ based on medical image data. These equations inherently involve a practical application and should be eligible and not be considered abstract under step 2A. It is noted that there are at least two subcategories of equations of this type that the courts have found not eligible. But in each case, these exceptions were found ineligible not because they were equations, but for other reasons. These sub-categories are described in section 2.2 and 2.3.
2.2 (Not eligible) Equations that evaluate a natural law.
These equations are only true if the variables in the equations relate to physical phenomena (thus not mathematical identities) but do express a natural law alone (e.g., correlation of physical phenomena in nature, such as, e=mc2). These are recognizable and distinguished from equations of type 2.1 because these equations are claimed as unrelated to whether a man-made object is involved, e.g., unrelated to whether a man-made device makes a measurement or not, or unrelated to whether a man-made device perturbs the environment or not. Each is ineligible, not as an abstract idea, but as directed to a natural law. Note that the Arrhenius equation adjudicated in Diamond v. Diehr, 450 U.S. 175, 188 (Diamond) is of this type. The draft Guidance states. The statement in Diamond appears to require an inventive step other than an equation. Diamond at 191. It should be noted that this is dictum because the claims were found to be eligible for reciting something more (under what is now known as step 2B), by operating a rubber molding device. Diamond at 191. The Court correctly noted that the Arrhenius equation is not patent eligible; but gave an overbroad statement, lumping all equations of different types into the same barrel. This overbroad statement need not be followed blindly; but, instead, should be confined to the facts of that case, which involve an equation citing a law of nature. Benson has already been discussed as directed to a mathematical identity of type 1.1.
2.3. (Not eligible) Equations involving only mental steps.
The equations in this category are equations that describe one or more mental steps that are typically/routinely/easily performed without a computer. Flook found an equation for an alarm limit to be patent ineligible. Flook at 594. The facts of Flook are consistent with ineligibility based on implementing mental step. Flook states “the computations can be made by pencil and paper calculations” and the adjudicated claim does not recite a processor or situation in which it is impractical to perform the steps mentally; thus, Flook should be limited to the mental steps exception and not stand for the proposition that all equations should be considered in the prior art; thus, making all claims directed to the use of equations on a computer ineligible. Flook at 586. The cases cited by Flook (Benson and Morse) do not support that conclusion; rather, those cases are related to citing a mathematical identity for equations of type 1.2 (Benson), and a natural law as described above for equation type 2.2 (Morse), respectively.
2.4. (Not eligible) Equations relating ineligible variables.
Equations that recite ineligible variables are only true if a variable in the equation relates to a particular property (thus not mathematical identities); but the particular property is not a physical phenomenon, and instead has been found by the courts to be abstract. Examples of properties found to be abstract by the courts, as listed in the draft Guidance, include certain methods of organizing human activity. These equations should not be eligible for patent protection because they involve variables or results that are specifically found to be abstract ideas. These are abstract, not because the equation is abstract; but, because of the other factors that render a claim abstract, namely, the variables x1, x2 … or result y, refer to abstract concepts. The organizing human activity portion of abstract ideas is the reason for unpatentable subject matter in many famous cases. Another example is SAP Am. Inc. v. InvestPic LLC, 898 F. 3d 1161 (Fed. Cir. 2018) cited in the draft Guidance, where the focus of the claims is analyzing data pertaining to investment. SAP at 1164-1165.
Figure 1 summarizes the above analysis of equations.
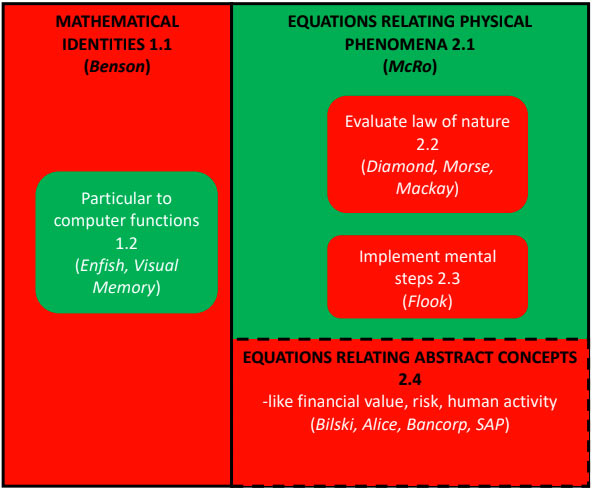
Figure 1. Venn diagram of mathematical equations. Red areas have been found patent ineligible in various cases. Green areas should be patent eligible as practical applications that are not abstract ideas.
